|
|
|
|
|
|
|
|
|
CHAPITRE 02 : THEOREME DE THALES.
 Objectifs Objectifs |
OBJECTIFS :
- Connaître et savoir utiliser dans une situation donnée, le théorème de Thalès ainsi que sa réciproque.
- Connaître les propriétés relatives à l’agrandissement et la réduction d’une figure.
- Connaître et savoir utiliser le fait que dans une réduction ou un agrandissement de rapport k, l’aire d’une surface est multipliée par $k^2$ ; le volume d’un solide par $k^3$.
Activités :
 Partie 1 Partie 1 |
I. THEOREME DE THALES.
Théorème 1 : Théorème de Thalès.
Soit $(d)$ et $(d')$ deux droites sécantes en A.
Soit B et M deux points de la droite $(d)$ distincts de A.
Soit C et N deux points de la droite $(d')$ distincts de A.
Si les droites $(BC)$ et $(MN)$ sont parallèles, alors on a : $(AM)/(AB)=(AN)/(AC)=(MN)/(BC)$.
Exemple 1 :
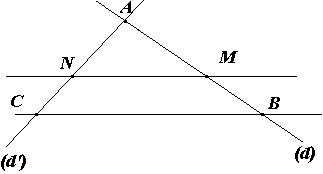
$AC=5$ cm ; $AN=3$ cm ; $AB=7$ cm et $(BC)////(MN)$
Sur la figure ci-dessus, on a : les droites $(d)$ et $(d')$ sécantes en A ; $N in (d')$ et $C in (d')$ ; $M in (d)$ et $B in (d)$.
Donc d’après le théorème de Thalès, on a : $(AM)/(AB)=(AN)/(AC)=(MN)/(BC)$.
D’où : $7/(AB)=5/3=(MN)/(BC)$.
En utilisant le produit en « T » ou « Y », il vient : $AM=(7xx3)/5=21/5=4,2$ cm.
Exemple 2 :
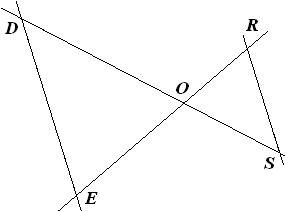
$DE=7,2$ cm ; $OE=4,5$ cm ; $RS=3,2$ cm et $(DE)////(RS)$
Sur la figure ci-dessus, on a : $O in (RE)$ et $O in (DS)$.
Donc d’après le théorème de Thalès, on a : $(OR)/(OE)=(OS)/(OD)=(RS)/(DE)$.
D’où : $(OR)/(4,5)=(OS)/(OD)=(3,2)/(7,2)$.
En utilisant le produit en « T » ou « Y », il vient : $OR=(4,5xx3,2)/(7,2)=(45xx32)/720=(9xx5xx8xx2xx2)/(9xx8xx2xx5)=2$ cm.
Proposition 1 : conséquence au théorème de Thalès.
Soit $(d)$ et $(d')$ deux droites sécantes en A.
Soit B et M deux points de la droite $(d)$ distincts de A.
Soit C et N deux points de la droite $(d')$ distincts de A.
Si $(AM)/(AB)!=(AN)/(AC)$, alors les droites $(BC)$ et $(MN)$ ne sont pas parallèles.
Exemple 3 :

$AB=10$ cm ; $AC=8$ cm ; $AN=3$ cm et $AM=4$ cm.
Sur la figure ci-dessus, on a : les droites $(CN)$ et $(MB)$ sécantes en A.
On a : $(AN)/(AC)=3/8=0,375$ et $(AM)/(AB)=4/10=0,4$.
Donc $(AM)/(AB)!=(AN)/(AC)$.
Par conséquence du théorème de Thalès, les droites $(BC)$ et $(MN)$ ne sont pas parallèles.
Exercices proposés : Exercices N°.
 Partie 2 Partie 2 |
II. RECIPROQUE AU THEOREME DE THALES.
Proposition 2 : réciproque au théorème de Thalès.
Soit $(d)$ et $(d')$ deux droites sécantes en A.
Soit B et M deux points de la droite $(d)$ distincts de A.
Soit C et N deux points de la droite $(d')$ distincts de A.
Si les points A, M et B d’une part et A, N et C d’autre part sont dans le même ordre et si $(AM)/(AB)=(AN)/(AC)$, alors les droites $(BC)$ et $(MN)$ sont parallèles.
Exemple 4 :

$OE=4,2$ cm ; $OS=2,8$ cm ; $OR=2,1$ cm et $OD=5,6$ cm.
Sur la figure ci-dessus, on a : O point d’intersection des droites $(RE)$ et $(DS)$.
les points D, O et S d’une part et E, O et R d’autre part sont dans le même ordre.
On a : $(DO)/(OS)=(5,6)/(2,8)=2$ et $(OE)/(OR)=(4,2)/(2,1)=2$.
Donc, d’après la réciproque au théorème de Thalès, les droites $(DE)$ et $(RS)$ sont parallèles.
Exercices proposés : Exercices N°.
 Partie 3 Partie 3 |
III. AGRANDISSEMENT ET REDUCTION
Définition 1 :
Un agrandissement (respectivement réduction) d’une figure $(cc(F))$ de rapport k est une figure $(cc(F'))$ dont toutes les longueurs sont proportionnelles à celles de la figure $(cc(F))$ où k est le coefficient de proportionnalité.
Remarque 1 :
Si $k>1$, alors c’est un agrandissement.
Si $k<1$, alors c’est une réduction.
Proposition 3 :
Lors d’un agrandissement ou d’une réduction, les angles de la figure $(cc(F'))$ ont la même mesure que ceux de la figure $(cc(F))$.
Exemple 5 :
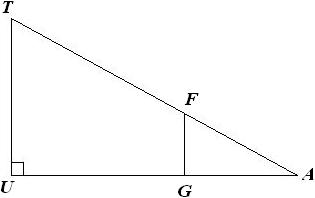
T, F et A sont alignés et U, G et A sont alignés. On donne : $AT=9,3$ cm, $AU=7,8$ cm, $TU=5,4$ cm, $AF=3,1$ cm, $AG=2,6$ cm et $FG=1,8$ cm.
 |
Longueurs du triangle TAU |
$AT=9,3$ cm |
$AU=7,8$ cm |
$TU=5,4$ cm |
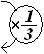 |
| Longueurs du triangle GAF |
$AF=3,1$ cm |
$AG=2,6$ cm |
$FG=1,8$ cm |
Ainsi toutes les longueurs des deux triangles TAU et GAF sont proportionnelles. Le triangle GAF est une réduction du triangle TAU, de rapport $k=1/3$.
De plus l’angle $hat(TUA)$ est droit ; par conséquence de la proposition 3, l’angle $hat(FGA)$ est droit lui aussi.
Proposition 4 :
Lors d’un agrandissement ou d’une réduction de rapport O, l’aire d’une surface est multipliée par $k^2$ et le volume d’un solide est multiplié par $k^3$.
Exemple 6 :
En reprenant l’exemple 5, trouvons l’aire des triangles TAU et GAF. Les triangles sont rectangles, donc :
$cc(A)_(TAU)=(TU xx UA)/2=(5,4xx7,8)/2=21,06$ cm2.
$cc(A)_(GAF)=(FG xx GA)/2=(1,8xx2,6)/2=2,34$ cm2.
Et nous avons bien : $(1/3)^2 xx cc(A)_(TAU)=1/9 xx 21,06=2,34$ cm2. Donc $cc(A)_(GAF)=(1/9)^2 xxcc(A)_(TAU)$.
Exercices proposés : Exercices N°.
|
|
 |
Ce site a fait l'objet d'une déclaration à la CNIL.
Vous disposez d'un droit d'accès, de modification et de suppression des données vous concernant (loi Informatique et Libertés du 6 janvier 1978).
Pour toute demande et pour exercer ce droit, adressez-vous à M. ETIENNE.
Ce site est une initiative expérimentale privée, il est totalement indépendant et ne saurait être considéré comme le reflet de la politique du collège Pablo Picasso. En aucun cas, la responsabilité de celui-ci ne pourrait être recherchée. |
|
|
|